문제
https://www.acmicpc.net/problem/2281
2281번: 데스노트
첫째 줄에 n(1 ≤ n ≤ 1,000), m(1 ≤ m ≤ 1,000)이 주어진다. m은 노트의 가로 칸의 개수(폭, 너비)이다. 다음 n개의 줄에는 각 사람의 이름의 길이가 노트에 적어야 할 순서대로 주어진다. 각 길이는 m
www.acmicpc.net
사악한 라이토는 기발한 방법을 이용하여 L(애칭 섊)을 살해한 뒤 데스노트를 다시 손에 넣었다. 라이토는 이제 이 노트에 n명의 이름을 적어 넣으려고 한다. 이때 다음과 같은 조건을 만족시키면서 이름을 적어 넣으려 한다.
우선, 이름을 적어 넣을 때 이미 정해진 순서대로 n명의 이름을 적어 넣어야 한다. 이름을 적을 때도, 노트를 위에서 아래로, 같은 줄에서는 왼쪽 맨 끝에서 오른쪽으로 차례로 적는다고 하자. 또한 이름을 적을 때 각 사람의 이름 사이에 빈 칸을 하나씩 두려고 한다. 한 줄을 적다가 그 줄의 끝에 한 사람의 이름이 다 들어가지 않고 잘리게 되면 반드시 새로운 줄에 이름을 써야 한다. 그렇지 않으면 이름이 중간에 잘려서 자칫하면 두 명의 사람이 죽게 된다. 이때, 각 줄의 끝에 사용하지 않고 남게 되는 칸의 수의 제곱의 합이 최소가 되도록 하려 한다. 이를 계산할 때 제일 마지막 줄은 앞으로 이름을 적을 기회가 있으므로 계산하지 않는다. 예를 들어 노트의 폭(너비)이 20인 다음의 경우를 보자.
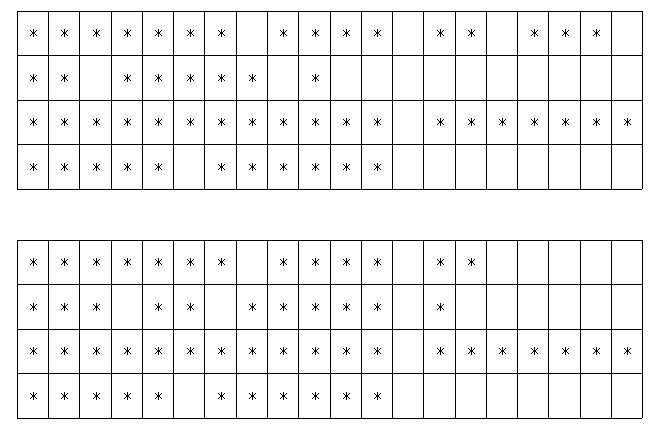
각 사람의 이름의 길이가 차례로 7, 4, 2, 3, 2, 5, 1, 12, 7, 5, 6 인 경우이다. 위와 같이 적으면 차례로 1, 10, 0칸이 남아서 제곱의 합이 101이 된다. 반면에 아래의 경우에는 5, 6, 0칸이 남아서 제곱의 합이 61이 된다.
입력
첫째 줄에 n(1 ≤ n ≤ 1,000), m(1 ≤ m ≤ 1,000)이 주어진다. m은 노트의 가로 칸의 개수(폭, 너비)이다. 다음 n개의 줄에는 각 사람의 이름의 길이가 노트에 적어야 할 순서대로 주어진다. 각 길이는 m을 넘지 않는 자연수이다.
출력
첫째 줄에 남게 되는 칸 수의 제곱의 합의 최솟값을 출력한다.
풀이
퇴사2 문제처럼 특정 시점 이후에 최댓값(이 문제에서는 최솟값)이 결정되는 문제인가?
-> 아니다. 이전 개행이 이후 최솟값에 영향을 미칠 수 있을 것 같다.
-> 모든 경우의 수를 탐색해야 할 것 같다.
-> 대신 시간복잡도를 줄이기 위해 dp를 사용해야 할 것 같다.
2차원 배열을 만들어서 내부에 최솟값을 저장하자
순차적으로 탐색해야 하는 값이 이 문제에서는 이름이랑 노트의 행 또는 열이었다.
이름 X 노트의 행
이름 X 노트의 열
중 어떤 값으로 dp를 만들지 고민하다가 열 값이 더 맞는 것 같아 그렇게 짰다.
풀이의 핵심은 이전에 이름이 쓰인 위치에서 다음 이름을 뒤에 붙여 적는 방법과 다음 줄에 적는 방법을 계산하여 반복하는 것이다.
3 9
7
4
2
의 예제로 예시를 들자면
먼저 모든 배열을 -1로 초기화하고(방문하지 않았다는 뜻) 맨 처음 이름의 값 위치를 0으로 초기화한다.
이 예제에서는 0,7 위치를 0으로 초기화 한다.
다음 이름을 쓸 때에는 다음 줄에 쓰는 방법과 이번 줄에 붙여서 쓰는 방법 두 가지가 있다.
다음 이름의 길이는 4이므로 7 뒤에 붙여 쓸 수 없으므로 새로운 줄에 쓴다.
이 때 다음 줄로 넘어갔으므로, 남은 공간의 제곱의 크기를 저장해준다.
이제 또 다음 줄로 넘어가서 붙여 쓰는 경우와 새 줄에 쓰는 경우를 계산해준다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 7 | -1 | -1 | -1 | -1 | -1 | -1 | 0 | -1 | -1 |
| 4 | -1 | -1 | -1 | 4 | -1 | -1 | -1 | -1 | -1 |
| 2 | -1 | -1 | 4+25 | -1 | -1 | 4 | -1 | -1 | -1 |
마지막 줄에서 -1을 제외하고 가장 작은 값을 출력하면 된다.
import sys
input = sys.stdin.readline
n, m = map(int, input().split())
names = [int(input()) for _ in range(n)]
dp = [[-1]*(m+1) for _ in range(n)]
dp[0][names[0]] = 0
for r in range(n-1):
for c in range(1, m+1):
if dp[r][c] != -1:
#뒤에 붙이는 경우의 수
if c+1+names[r+1] <= m:
dp[r+1][c+names[r+1]+1] = dp[r][c]
#다음줄에 쓰는 경우의 수
if dp[r+1][names[r+1]] != -1:
dp[r+1][names[r+1]] = min(dp[r+1][names[r+1]], dp[r][c] + (m-c)**2)
else:
dp[r+1][names[r+1]] = dp[r][c] + (m-c)**2
answer = 1000000000
for i in range(1, m+1):
if dp[n-1][i] != -1:
answer = min(answer, dp[n-1][i])
print(answer)
좀 고민을 했지만 맞게 풀고 있는 줄은 몰랐는데 바로 성공해서 뿌듯하다
dp 조금은 알 것 같기도 하고..
'알고리즘 스터디' 카테고리의 다른 글
| [백준] 10422 괄호 - 파이썬 (0) | 2022.02.20 |
|---|---|
| [백준] 2616 소형기관차 - 파이썬 (0) | 2022.02.14 |
| [백준] 5557 1학년 - 파이썬 (0) | 2022.02.08 |
| [백준] 12026 BOJ 거리 - 파이썬 (0) | 2022.02.06 |
| [백준] 11058 크리보드 파이썬 (0) | 2022.02.02 |