문제
https://www.acmicpc.net/problem/17070
17070번: 파이프 옮기기 1
유현이가 새 집으로 이사했다. 새 집의 크기는 N×N의 격자판으로 나타낼 수 있고, 1×1크기의 정사각형 칸으로 나누어져 있다. 각각의 칸은 (r, c)로 나타낼 수 있다. 여기서 r은 행의 번호, c는 열의
www.acmicpc.net
유현이가 새 집으로 이사했다. 새 집의 크기는 N×N의 격자판으로 나타낼 수 있고, 1×1크기의 정사각형 칸으로 나누어져 있다. 각각의 칸은 (r, c)로 나타낼 수 있다. 여기서 r은 행의 번호, c는 열의 번호이고, 행과 열의 번호는 1부터 시작한다. 각각의 칸은 빈 칸이거나 벽이다.
오늘은 집 수리를 위해서 파이프 하나를 옮기려고 한다. 파이프는 아래와 같은 형태이고, 2개의 연속된 칸을 차지하는 크기이다.

파이프는 회전시킬 수 있으며, 아래와 같이 3가지 방향이 가능하다.

파이프는 매우 무겁기 때문에, 유현이는 파이프를 밀어서 이동시키려고 한다. 벽에는 새로운 벽지를 발랐기 때문에, 파이프가 벽을 긁으면 안 된다. 즉, 파이프는 항상 빈 칸만 차지해야 한다.
파이프를 밀 수 있는 방향은 총 3가지가 있으며, →, ↘, ↓ 방향이다. 파이프는 밀면서 회전시킬 수 있다. 회전은 45도만 회전시킬 수 있으며, 미는 방향은 오른쪽, 아래, 또는 오른쪽 아래 대각선 방향이어야 한다.
파이프가 가로로 놓여진 경우에 가능한 이동 방법은 총 2가지, 세로로 놓여진 경우에는 2가지, 대각선 방향으로 놓여진 경우에는 3가지가 있다.
아래 그림은 파이프가 놓여진 방향에 따라서 이동할 수 있는 방법을 모두 나타낸 것이고, 꼭 빈 칸이어야 하는 곳은 색으로 표시되어져 있다.
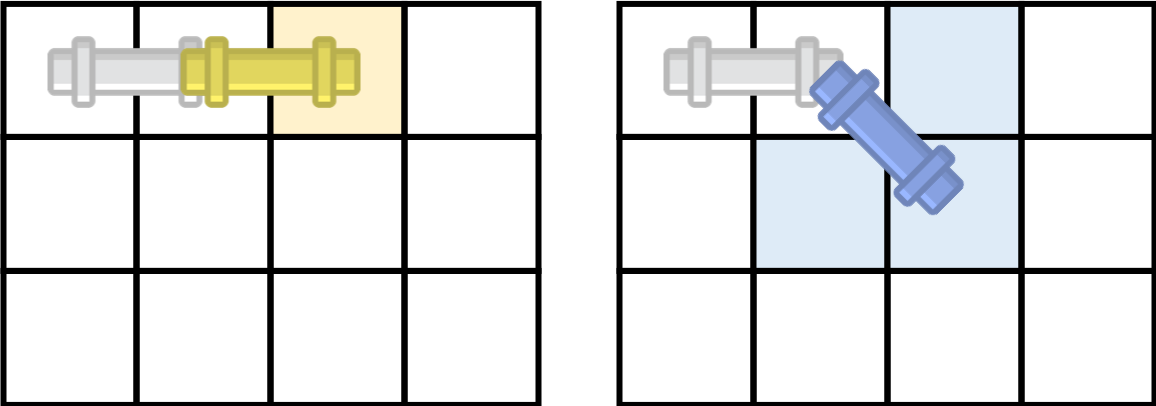
가로

세로

대각선
가장 처음에 파이프는 (1, 1)와 (1, 2)를 차지하고 있고, 방향은 가로이다. 파이프의 한쪽 끝을 (N, N)로 이동시키는 방법의 개수를 구해보자.
입력
첫째 줄에 집의 크기 N(3 ≤ N ≤ 16)이 주어진다. 둘째 줄부터 N개의 줄에는 집의 상태가 주어진다. 빈 칸은 0, 벽은 1로 주어진다. (1, 1)과 (1, 2)는 항상 빈 칸이다.
출력
첫째 줄에 파이프의 한쪽 끝을 (N, N)으로 이동시키는 방법의 수를 출력한다. 이동시킬 수 없는 경우에는 0을 출력한다. 방법의 수는 항상 1,000,000보다 작거나 같다.
풀이
두 가지의 풀이 방법이 떠올랐다.
1. dp
세 가지 타입의 보드를 만든다.
보드에는 해당 칸까지 해당 타입으로 올 수 있는 방법의 수를 저장한다.
가로형태, 세로형태, 대각선 타입의 보드를 각각 만들어
총 n-1,n-1 칸에 갈 수 있는 방법의 수를 구한다.
이 방법으로 구현은 하지 않아 구현 시 문제가 없을지는 잘 모르겠다.
2. bfs 혹은 dfs
큐에 좌표와 파이프가 놓여 있는 타입을 저장하여 탐색을 진행한다.
n-1,n-1에 도착하면 cnt+1을 한다.
큐가 빌 때 까지 탐색을 진행하고 cnt를 프린트한다.
어차피 전체 탐색을 해야 하기 때문에 bfs나 dfs나 상관 없다고 생각했다.
dp방법보다 구현이 쉬울 것 같아 bfs로 먼저 구현했는데 63%쯤에서 시간초과가 발생했다.
import sys
from collections import deque
input = sys.stdin.readline
n = int(input())
board = [list(map(int, input().split())) for _ in range(n)]
HO = 0
VIR = 1
DIAG = 2
q = deque([(0, 1, HO)])
cnt = 0
while q:
nowy, nowx, type = q.popleft()
if (nowy, nowx) == (n-1, n-1):
cnt += 1
continue
if type == HO or type == DIAG:
if nowx+1 < n and board[nowy][nowx+1] == 0:
q.append((nowy, nowx+1, HO))
if type == VIR or type == DIAG:
if nowy + 1 < n and board[nowy+1][nowx] == 0:
q.append((nowy+1, nowx, VIR))
if nowx+1<n and nowy+1<n:
if board[nowy+1][nowx] == 0 and board[nowy][nowx+1] == 0 and board[nowy+1][nowx+1] == 0:
q.append((nowy+1, nowx+1, DIAG))
print(cnt)dp로 다시 풀어야하나 고민하다가 다른 사람 코드를 보았는데
동일한 로직에 bfs로 푼 분이 통과하신 코드가 있었다.
https://chldkato.tistory.com/165
백준 17070 파이프 옮기기 1 (파이썬)
https://www.acmicpc.net/problem/17070 17070번: 파이프 옮기기 1 유현이가 새 집으로 이사했다. 새 집의 크기는 N×N의 격자판으로 나타낼 수 있고, 1×1크기의 정사각형 칸으로 나누어져 있다. 각각의 칸은 (r,
chldkato.tistory.com
deque를 사용해서 시간이 더 들었던걸까..!
코드를 조금 바꿔 dfs로 풀어보기로 했다.
import sys
input = sys.stdin.readline
n = int(input())
board = [list(map(int, input().split())) for _ in range(n)]
HO = 0 #가로
VIR = 1 #세로
DIAG = 2 #대각
cnt = 0
def dfs(nowy, nowx, type):
global cnt
if (nowy, nowx) == (n-1, n-1):
cnt += 1
return
if type == HO or type == DIAG:
if nowx+1 < n and board[nowy][nowx+1] == 0:
dfs(nowy, nowx+1, HO)
if type == VIR or type == DIAG:
if nowy + 1 < n and board[nowy+1][nowx] == 0:
dfs(nowy+1, nowx, VIR)
if nowx+1<n and nowy+1<n:
if board[nowy+1][nowx] == 0 and board[nowy][nowx+1] == 0 and board[nowy+1][nowx+1] == 0:
dfs(nowy+1, nowx+1, DIAG)
dfs(0, 1, HO)
print(cnt)정말 통과했다..
완전탐색을 할 땐 dfs가 더 빨랐다..!
deque를 사용하지 않아서 그런 거로 추측
'알고리즘 스터디' 카테고리의 다른 글
| [백준] 1303 전투 - 파이썬 (0) | 2021.12.24 |
|---|---|
| [백준] 1260 DFS와 BFS - 파이썬 (0) | 2021.12.24 |
| [백준] 1038 감소하는 수 파이썬 (0) | 2021.12.12 |
| [백준] 2667 단지번호붙이기 파이썬 (0) | 2021.12.12 |
| [백준] 2294 동전2 파이썬 (0) | 2021.12.12 |