문제
원점(0,0)에서 시작해서 아래처럼 숫자가 적힌 방향으로 이동하며 선을 긋습니다.
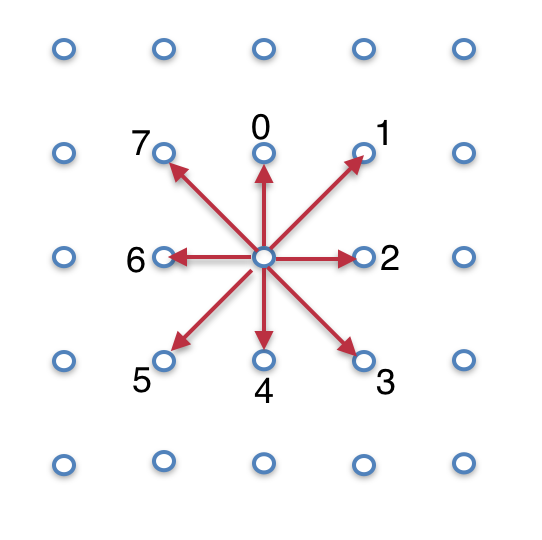
ex) 1일때는 오른쪽 위로 이동
그림을 그릴 때, 사방이 막히면 방하나로 샙니다.
이동하는 방향이 담긴 배열 arrows가 매개변수로 주어질 때, 방의 갯수를 return 하도록 solution 함수를 작성하세요.
제한사항
- 배열 arrows의 크기는 1 이상 100,000 이하 입니다.
- arrows의 원소는 0 이상 7 이하 입니다.
- 방은 다른 방으로 둘러 싸여질 수 있습니다.
입출력 예
arrowsreturn
| [6, 6, 6, 4, 4, 4, 2, 2, 2, 0, 0, 0, 1, 6, 5, 5, 3, 6, 0] | 3 |
입출력 예 설명

- (0,0) 부터 시작해서 6(왼쪽) 으로 3번 이동합니다. 그 이후 주어진 arrows 를 따라 그립니다.
- 삼각형 (1), 큰 사각형(1), 평행사변형(1) = 3
코딩테스트 연습 - 방의 개수
[6, 6, 6, 4, 4, 4, 2, 2, 2, 0, 0, 0, 1, 6, 5, 5, 3, 6, 0] 3
programmers.co.kr
풀이
딱 떠오르는 풀이 방법이 없었다.
방이 생기는 조건으로 한 점을 두 번 방문하는지 확인하면 될까 싶었는데
예외상황이 많이 발생할 것 같았다.
크루스칼이나 프라임처럼 어떠한 풀이 방법이 있는 것이 아닐까 싶어 검색하다
(https://pf333.tistory.com/86) 이 분 글을 참고했다.
특정한 알고리즘 문제는 아니었고
다만 예외상황을 잘 처리해야 하는 문제였다.
같은 점을 두 번 방문할 때 방의 개수를 1씩 늘려주는 것은 맞으나
다음과 같은 두 가지의 주요한 예외가 있다.
- 점을 같은 경로로 방문했을 때에는 방이 생기지 않는다.
- 모래시계 형태의 방이 생길 수 있다.
2번 상황은 위의 블로그 링크의 그림을 보면 이해하기 쉽다.
1번 예외상황을 처리하기 위해 way 배열을 만들고 각각 방문한 경로를 저장했다.
솔루션 함수 내의 포문에서 찍어보았다. way는 위와 같은 형태로 저장된다.
만약 같은 경로로 들어왔다면, 방의 개수를 늘리지 않고 무시한다.
2번 예외를 처리하기 위해서 대각선으로 이동할 때, 중간 점을 하나 더 만들어 저장해줬다.
중간에 점을 하나 더 만들고 거기서도 같은 점에 다른 경로로 들어오는지 체크하여 방의 개수를 업데이트해줬다.
def solution(arrows):
answer = 0
dirc = [(0, -1), (1, -1), (1, 0), (1, 1), (0, 1), (-1, 1), (-1, 0), (-1,-1)]
way = {(0,0): []}
now = (0,0)
def saveway(a, now, delta):
nonlocal answer
if now not in way:
way[now] = [a]
else:
way[now].append(a)
now = (now[0] + delta[0], now[1] + delta[1])
b = a-4 if a >= 4 else a+4 #진입한 경로
if now not in way:
way[now] = [b]
else:
if b not in way[now]:
answer += 1
way[now].append(b)
return now
for a in arrows:
if abs(dirc[a][0]) + abs(dirc[a][1]) >= 2: #모래시계 형태를 처리하기 위해
now = saveway(a, now, (dirc[a][0]/2, dirc[a][1]/2))
now = saveway(a, now, (dirc[a][0]/2, dirc[a][1]/2))
else:
now = saveway(a, now, (dirc[a][0], dirc[a][1]))
return answer
다른 사람의 풀이
def solution(arrows):
point=set([(0,0)])
line=set()
move=[[0,2],[2,2],[2,0],[2,-2],[0,-2],[-2,-2],[-2,0],[-2,2]]
pre_point=(0,0)
for A in arrows:
next_point=(pre_point[0]+move[A][0], pre_point[1]+move[A][1] )
mid_point=(pre_point[0]+move[A][0]//2, pre_point[1]+move[A][1]//2 )
point.add(next_point)
point.add(mid_point)
line.add((pre_point,mid_point))
line.add((mid_point,pre_point))
line.add((mid_point,next_point))
line.add((next_point,mid_point))
pre_point=next_point
answer = len(line)//2-len(point)+1
return answer if answer>=0 else 0오일러 공식을 사용한 풀이라고 한다.
마지막 answer 부분 이해가 안 간다.
누가 설명해줄 사람,,?👀
'알고리즘 스터디' 카테고리의 다른 글
| [백준] 준비운동 Part1. 튼튼한 기본기2 (0) | 2021.09.25 |
|---|---|
| [백준] 준비운동 Part1. 튼튼한 기본기1 (0) | 2021.09.11 |
| [프로그래머스] 이분탐색 2. 징검다리 (0) | 2021.08.26 |
| [프로그래머스] DFS/BFS 4. 여행경로 (0) | 2021.08.20 |
| [프로그래머스] 탐욕법 6. 단속 카메라 (0) | 2021.08.07 |